NumPy支持大量的维度数组与矩阵运算,是针对数组运算的Python库。
本文收录于机器学习前置教程系列。
一、Python基础
我们首先巩固一下Python的基础知识。Python有6种标准数据类型:Number(数字),String(字符串),List(列表),Tuple(元组),Set(集合),Dictionary(字典)。
其中:
不可变数据:Number(数字)、String(字符串)、Tuple(元组)。
可变数据:List(列表)、Dictionary(字典)、Set(集合)。
1. List[列表]
列表由方括号 [ ] 包裹,每个位置的数值可变。
list = [1, 2, 3, 4, 5, 6]
根据位置取值,如取第2个位置的值:
list[1]
得到 2。
从第3个位置取值,到列表末尾的所有值:
a[2:]
得到 [3, 4, 5, 6]。
改变指定位置的值:
list[0] = 9
列表a此时输出为 [9, 2, 3, 4, 5, 6]。
2. Tuple(元组)
元组由圆括号 ( ) 包裹,每个位置的数值不可变。允许数据重复。
tuple = ('a', 'a, 'c', 1, 2, 3.0)
输出('a', 'a', 'c', 1, 2, 3.0)。
取最后一个位置的元素:
tuple[-1]
输出 3.0。
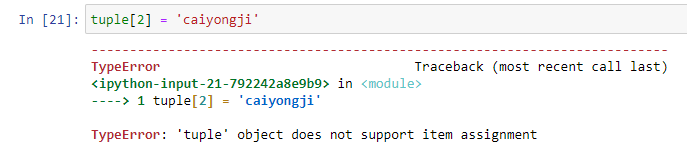
元组操作与列表类似,但不可改变元组内元素的值,否则会报错。
tuple[2] = 'caiyongji'
3. Set{集合}
集合是包含不重复元素的集体,由花括号 { } 包裹。
set1 = {'a','b','c','a'}
set2 = {'b','c','d','e'}
set1的输出结果为:{'a', 'b', 'c'}。注意:集合会删除重复元素。
set2的输出结果为:{'b', 'c', 'd', 'e'}。
与列表和元组不同,集合是不可下标的,如:
set1[0]

下面,我们来看看集合运算。
set1和set2的差集:
set1 - set2
#set1.difference(set2)
输出:{'a'}。
set1和set2的并集:
set1 | set2
#set1.union(set2)
输出:{'a', 'b', 'c', 'd', 'e'}。
set1和set2的交集:
set1 & set2
#set1.intersection(set2)
输出:{'b', 'c'}。
set1和set2的对称差集:
set1 ^ set2
#(set1 - set2) | (set2 - set1)
#set1.symmetric_difference(set2)
输出:{'a', 'd', 'e'}。
以上差集、并集、交集、对称差集都有对应的集合方法,可以注释方法自己试试。
4. Dictionary{字典:Dictionary}
字典是一种映射关系,是无序有键值对(key-value)集合。字典不允许重复的键(key),但允许重复的值(value)。
dict = {'gongzhonghao':'caiyongji','website':'caiyongji.com', 'website':'blog.caiyongji.com'}
字典输出{'gongzhonghao': 'caiyongji', 'website': 'blog.caiyongji.com'},需要注意的是,当字典包含重复键,后面的会覆盖前面的元素。
dict['gongzhonghao']
输出字符串 caiyongji。我们也可以使用get方法得到相同效果。
dict.get('gongzhonghao')
查看所有的键(key):
dict.keys()
输出 dict_keys(['gongzhonghao', 'website'])。
查看所有的值(value):
dict.values()
输出 dict_values(['caiyongji', 'blog.caiyongji.com'])。
改变某一项的值:
dict['website'] = 'caiyongji.com'
dict
输出 {'gongzhonghao': 'caiyongji', 'website': 'caiyongji.com'}。
了解了Python的数据类型,我们可以学着使用NumPy了。
二、Numpy常见用法
1. 创建数组
import numpy as np
arr = np.array([1, 2, 3, 4, 5])
arr的输出为array([1, 2, 3, 4, 5])。
我们输入以下代码创建二维数组:
my_matrix = [[1,2,3],[4,5,6],[7,8,9]]
mtrx= np.array(my_matrix)
mtrx的输出如下:
array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
2. 索引与切片
索引一维数组与二位数组如下:
print('arr[0]=',arr[0],'mtrx[1,1]=',mtrx[1,1])
输出 arr[0]= 1 mtrx[1,1]= 5。
对数组切片:
arr[:3]
输出结果为 array([1, 2, 3])。
倒数切片:
arr[-3:-1]
输出 array([3, 4])。
加入步长(step),步长决定了切片间隔:
arr[1:4:2]
输出 array([2, 4])。
二维数组切片:
mtrx[0:2, 0:2]
输出,代码意义为取第1、2行,第1、2列:
array([[1, 2],
[4, 5]])
3. dtype
NumPy的dtpe有如下几种数据类型:
- i - integer
- b - boolean
- u - unsigned integer
- f - float
- c - complex float
- m - timedelta
- M - datetime
- O - object
- S - string
- U - unicode string
- V - fixed chunk of memory for other type ( void )
import numpy as np
arr1 = np.array([1, 2, 3, 4])
arr2 = np.array(['apple', 'banana', 'cherry'])
print('arr1.dtype=',arr1.dtype,'arr2.dtype=',arr2.dtype)
输出为 arr1.dtype= int32 arr2.dtype= <U6。arr1数据类型为int32,arr2的<U6表示不超过6位Unicode字符串。
我们可以指定dtype类型。
arr = np.array(['1', '2', '3'], dtype='f')
输出结果位 array([1., 2., 3.], dtype=float32),其中1.表示1.0,可以看到dtype被设置位float32数据类型。
4. 一般方法
4.1 arange
np.arange(0,101,2)输出结果如下,该命令表示,在[0,101)区间内均匀地生成数据,间隔步长为2。
array([ 0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24,
26, 28, 30, 32, 34, 36, 38, 40, 42, 44, 46, 48, 50,
52, 54, 56, 58, 60, 62, 64, 66, 68, 70, 72, 74, 76,
78, 80, 82, 84, 86, 88, 90, 92, 94, 96, 98, 100])
4.2 zeros
np.zeros((2,5))输出结果如下,该命令表示,输出2行5列全为0的矩阵(二维数组)。
array([[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.]])
4.3 ones
np.ones((4,4))输出结果如下,该命令表示,输出4行4列全为1的矩阵。
array([[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.]])
4.4 eye
np.eye(5)输出结果如下,该命令表示,输出对角线为1其余全为0的5行5列方阵。方阵为行列相同的矩阵。
array([[1., 0., 0., 0., 0.],
[0., 1., 0., 0., 0.],
[0., 0., 1., 0., 0.],
[0., 0., 0., 1., 0.],
[0., 0., 0., 0., 1.]])
4.5 rand
np.random.rand(5,2) 命令生成5行2列的随机数。
array([[0.67227856, 0.4880784 ],
[0.82549517, 0.03144639],
[0.80804996, 0.56561742],
[0.2976225 , 0.04669572],
[0.9906274 , 0.00682573]])
如果想保证随机出与本例一样的随机数,可使用与本例相同的随机种子。通过np.random.seed方法设置。
np.random.seed(99)
np.random.rand(5,2)
4.6 randint
np.random.randint(0,101,(4,5))输出结果如下,该命令表示,在[0,101)区间内随机选取整数生成4行5列的数组。
array([[ 1, 35, 57, 40, 73],
[82, 68, 69, 52, 1],
[23, 35, 55, 65, 48],
[93, 59, 87, 2, 64]])
4.7 max min argmax argmin
我们先随机生成一组数:
np.random.seed(99)
ranarr = np.random.randint(0,101,10)
ranarr
输出:
array([ 1, 35, 57, 40, 73, 82, 68, 69, 52, 1])
查看最大最小值分别为:
print('ranarr.max()=',ranarr.max(),'ranarr.min()=',ranarr.min())
输出结果为ranarr.max()= 82 ranarr.min()= 1。
其中最大值和最小值的索引位置分别为:
print('ranarr.argmax()=',ranarr.argmax(),'ranarr.argmin()=',ranarr.argmin())
输出:ranarr.argmax()= 5 ranarr.argmin()= 0。注意,当出现多个最大最小值时,取前面的索引位置。
三、NumPy进阶用法
1. reshape
arr = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12])
newarr = arr.reshape(4, 3)
其中,arr为一维数组,newarr为二位数组,其中行为4,列为3。
print('arr.shape=',arr.shape,'newarr.shape=',newarr.shape)
输出 arr.shape= (12,) newarr.shape= (4, 3)。
newarr的输出结果如下:
array([[ 1, 2, 3],
[ 4, 5, 6],
[ 7, 8, 9],
[10, 11, 12]])
2. 合并与分割
2.1 concatenate
一维数组合并:
arr1 = np.array([1, 2, 3])
arr2 = np.array([4, 5, 6])
arr = np.concatenate((arr1, arr2))
arr
输出: array([1, 2, 3, 4, 5, 6])。
二维数组合并:
arr1 = np.array([[1, 2], [3, 4]])
arr2 = np.array([[5, 6], [7, 8]])
arr = np.concatenate((arr1, arr2))
arr
输出为:
array([[1, 2],
[3, 4],
[5, 6],
[7, 8]])
我们添加参数axis=1:
arr1 = np.array([[1, 2], [3, 4]])
arr2 = np.array([[5, 6], [7, 8]])
arr = np.concatenate((arr1, arr2), axis=1)
arr
输出为:
array([[1, 2, 5, 6],
[3, 4, 7, 8]])
我们把鼠标移到 concatenate,按快捷键Shift+Tab查看方法说明。可以看到concatenate方法沿着现有的轴进行合并操作,默认axis=0。当我们设置axis=1后,合并操作沿着列进行。

2.2 array_split
分割数组:
arr = np.array([[1, 2], [3, 4], [5, 6], [7, 8], [9, 10], [11, 12]])
newarr = np.array_split(arr, 3)
newarr
newarr的值为:
[array([[1, 2],
[3, 4]]),
array([[5, 6],
[7, 8]]),
array([[ 9, 10],
[11, 12]])]
3. 搜索与筛选
3.1 搜索
NumPy可通过where方法查找满足条件的数组索引。
arr = np.array([1, 2, 3, 4, 5, 6, 7, 8])
x = np.where(arr%2 == 0)
x
输出:
(array([1, 3, 5, 7], dtype=int64),)
3.2 筛选
我们看看下面的代码:
bool_arr = arr > 4
arr[bool_arr]
输出:array([5, 6, 7, 8])。这回我们返回的是数组中的值,而非索引。
我们看看bool_arr的内容究竟是什么。
bool_arr的输出为:
array([False, False, False, False, True, True, True, True])
所以我们可以用以下命令代替以上筛选。
arr[arr > 4]
4. 排序
sort方法可对ndarry数组进行排序。
arr = np.array(['banana', 'cherry', 'apple'])
np.sort(arr)
输出排序后的结果:array(['apple', 'banana', 'cherry'], dtype='<U6')。
针对二维数组,sort方法对每一行单独排序。
arr = np.array([[3, 2, 4], [5, 0, 1]])
np.sort(arr)
输出结果:
array([[2, 3, 4],
[0, 1, 5]])
5. 随机
5.1 随机概率
如果我们想完成如下需求该如何处理?
生成包含100个值的一维数组,其中每个值必须为3、5、7或9。 将该值为3的概率设置为0.1。 将该值为5的概率设置为0.3。 将该值为7的概率设置为0.6。 将该值为9的概率设置为0。
我们用如下命令解决:
random.choice([3, 5, 7, 9], p=[0.1, 0.3, 0.6, 0.0], size=(100))
输出结果:
array([7, 5, 7, 7, 7, 7, 5, 7, 5, 7, 7, 5, 5, 7, 7, 5, 3, 5, 7, 7, 7, 7,
7, 7, 7, 7, 7, 7, 5, 3, 7, 5, 7, 5, 7, 3, 7, 7, 3, 7, 7, 7, 7, 3,
5, 7, 7, 5, 7, 7, 5, 3, 5, 7, 7, 5, 5, 5, 5, 5, 7, 7, 7, 7, 7, 5,
7, 7, 7, 7, 7, 5, 7, 7, 7, 7, 3, 7, 7, 5, 7, 5, 7, 5, 7, 7, 5, 7,
7, 7, 7, 7, 7, 3, 5, 5, 7, 5, 7, 5])
5.2 随机排列
5.2.1 permutation
根据原有数组生成新的随机排列。
np.random.seed(99)
arr = np.array([1, 2, 3, 4, 5])
new_arr = np.random.permutation(arr)
new_arr
输出为:array([3, 1, 5, 4, 2])。原数组arr不变。
5.2.2 shuffle
改变原有数组为随机排列。shuffle在英文中有洗牌的意思。
np.random.seed(99)
arr = np.array([1, 2, 3, 4, 5])
np.random.shuffle(arr)
arr
输出为:array([3, 1, 5, 4, 2])。原数组arr改变。
5.3 随机分布
5.3.1 正太分布
使用np.random.normal方法生成符合正太分布的随机数。
x = np.random.normal(loc=1, scale=2, size=(2, 3))
x
输出结果为:
array([[ 0.14998973, 3.22564777, 1.48094109],
[ 2.252752 , -1.64038195, 2.8590667 ]])
如果我们想查看x的随机分布,需安装seaborn绘制图像。使用pip安装:
pip install -i https://pypi.tuna.tsinghua.edu.cn/simple seaborn
import matplotlib.pyplot as plt
import seaborn as sns
sns.distplot(x, hist=False)
plt.show()

5.3.2 二项分布
使用np.random.binomial方法生成符合二项分布的随机数。
x = np.random.binomial(n=10, p=0.5, size=10)
x
输出结果为: array([8, 6, 6, 2, 5, 5, 5, 5, 3, 4])。
绘制图像:
import matplotlib.pyplot as plt
import seaborn as sns
sns.distplot(x, hist=True, kde=False)
plt.show()

5.3.3 多项式分布
多项式分布是二项分布的一般表示。使用np.random.multinomial方法生成符合多项式分布的随机数。
x = np.random.multinomial(n=6, pvals=[1/6, 1/6, 1/6, 1/6, 1/6, 1/6])
x
上面代码,我们可以简单理解为投掷骰子。n=6为骰子的面,pvals表示每一面的概率为1/6。
5.3.4 其他
除以上分布外还有泊松分布、均匀分布、指数分布、卡方分布、帕累托分布等。感兴趣的可自行搜索。
本文收录于机器学习前置教程系列。欢迎大家点赞、收藏、关注,更多关于机器学习的精彩内容持续更新中……!